web6047 - 2025年 5月
ここは個人の趣味のページです。
私がプログラミングを好むわけは、プログラミングは私の「物づくり」に対する探求心と創造性を十分に満たしてくれるからです。
- 探求心:
ファミコン版「ドラゴンクエスト」に衝撃を受け、憧れて、そのための断片的なプログラムを作ることを楽しんできました。
断片的なプログラムとは、「マップを描画するだけ」とか、「プレイヤーキャラを動かすだけ」とかです。
そういう憧れに向かうステップ(探求)に、心躍る喜びがありました。 - 創造性:
この創造性とはアイデアを形にする喜びのことです。
もともと自分のアイデアを形にする「ペーパークラフト」や「木工」などのモノ作りが好きだったので、プログラミングとの相性が良かったようです。
ここの管理人、
AI の利用やめるってよ。
AI の問題点:
- 自分で考えずに AI を利用することで、考える力が減退する。
- 人と人との交流(教わる)が減る。
- 創作物のオリジナリティが無くなる。(自分の力で作ることの喜びが減る)
- 犯罪に使われている。
これらが向こう10年解決されないだろうと見込んで、やめることにしました。(2025年5月23日~)
私は AI に頼らず「自分の力」を大切にしたいです。
…とはいえ、人間は新しく見つけた技術を手放すということは基本的にやらないと思います。
だから私も後々 AI を利用することにはなると思います。
でも上記の問題点は確かなもので、将来 AI ロボが私の家の扉をコンコンと叩いて
「市からの要請で、お手伝いするため おうかがいしました」
と言うまでの間は、この AI 技術を導入せず、頑張ってみようと思います。
でもこの考え方、キツイと思うのでマネしなくていいです。
- Special Documents -
特別な記事へのリンク
ゲームコーナー
その他 単発のアプリ
- 以降は日記です -

2025年5月6日
事業会計 消費税の説明、本当?
今までこのサイトで消費税について、
「消費税は、飲んだ、食べた、自分のために購入したという消費について徴収するもの」
「製造者は原材料を消費するわけではないので仕入れ時に支払った消費税は取り返せる(控除できる)」
…と説明をしてきましたが、本当にそう考えて良いのかなと心配になり、いくつか調べてみました。
間違ったことをもっともらしく説明して、
『なんと!まちがっていた!、、、かも!』
とハラハラしています。今すぐ確認しないと…!!
(結果的には、上記の表現は「おおむね正しい」と結論しています)
1/4. 消費税という言葉
消費税とは、買い物をしたときに 10% 多めに取られるやつです。
………誰でも知ってるか………
お客さんたちは当たり前で消費税を払っていますが、店側は受け取った消費税を国に納税しています。
納税とは具体的には、店の担当者が役所窓口へ行って現金で支払うことで納税となります。
最近は自動引き落としとかになっています。
まず「消費税」とは、Wikipedia で、
消費税は、商品の販売やサービスの提供などの取引に対して課される租税である。
…と説明されています。
つまり、「消費税は、店が何かを売って、客がそれを買ったときに、その買い物について、国に対して買い物ができることの感謝の気持ちをお金を支払うことで示す」、ということです。← 少し冗談交じりで書いていますが、、
▼確認のため Grok(AI)に聞いてみました。

買い物は、道路や、交通機関、警察などもあって初めて安心してできますからね。
税金という形でお金を支払って感謝しなきゃいけないわけですよ。
酒を飲んで、プハーッうまい!
この気持ちを誰に伝えたいですか?
税金の形で国に伝えたいです!というやつはいないです。たぶん一人も。
……しかし、私が書いたように「消費者の飲み食いについて課されている」とは書かれておらず、「店側の販売に課されている」と書かれています。
goo辞書の "消費税" のページでは、
…と説明されています。
この説明の 1 行目は「消費に対して課される」と 消費者側 として書かれており、「店側の販売取引に課税」と言っている Wikipedia とは対照的です。
でも 2 行目では「原則としてすべての物品・サービスを課税」(店側)とも言っていて、gooの説明はちぐはぐとしています。
(※ 説明の中の「個別消費税」、というのは酒税とかタバコ税とかのことです。酒とかは特別に税が掛けられています)
2/4. 法律の言う消費税の課税対象はなんと!
「何について消費税が課税されるのか」、各辞書ではいまいちはっきりとしません。
そこで実際の消費税法を調べてみました。
(納税義務者)
第五条
事業者は、国内において行つた課税資産の譲渡等及び特定課税仕入れにつき、この法律により、消費税を納める義務がある。
これをわかりやすく言うと、
「店(事業者)は、商品の販売(課税資産の譲渡)につき、消費税を納める義務がある」
つまり、法律としては、消費税は「店側の商品の販売」が課税の対象なんですね。
買い物や飲み食いなどの「消費者の消費行為」ではありません。
消費税なのに、法律レベルで消費者の話をしていません!おどろきです。
そうだったのか!
Wikipedia と goo の説明を比べると、goo の言っていることも おおむね正しいですけど、Wikipedia の方がより正しいようです。
法律の言う消費税の課税対象は、消費者側ではなく、「店側の商品販売」です。
3/4. ただし、消費税の設計としては
ただし、消費税の「設計」としては、「最終的に商品やサービスを "消費する人" が負担するように設計されている」、と言われています。
(消費税は)最終的に消費者が負担する税であり、課税ベースが広く、また、税の累積を排除するために、仕入段階に係る税を控除できるという特質を持つ。
一般的に間接税(消費税など)は、製造者や流通業者の転嫁を通じて、最終的に消費者がその税を負担することが予定されている。
法律では法律の実用上の便宜を図って「店側の販売について消費税を課す」としていますが、設計が求めるのはあくまでも「消費者に課税」なのです。
ここでちょっと息抜き。生成 AI たちにお願いしました。
4/4. まとめ:私の説明は正しいのか
「飲んだ、食べた、自分のために購入した」という私の表現はたいへん庶民的ですが、確かに「消費」について説明しています。
上記の引用に書かれているように国税庁などは、そういう消費について「税が課税されるよう予定(=設計)されている」と言っています。
また、製造者は商品の製造のために原材料を仕入れします。その仕入れのときにも消費税は支払われますが、引用の通り 消費者とは「最終的な場所に位置する人のこと」を言っているので、製造での仕入れ(中間取引)は消費(最終消費)ではないと言えます。
…というわけで私の言っている
「消費税は、飲んだ、食べた、自分のために購入したという消費について徴収するもの。製造者は原材料を消費するわけではないので仕入時に支払った消費税は取り返せる(控除できる)」
…はおおむね正しいと言えます。
ハラハラはヒヤヒヤに変わりました。胸をなでおろすというやつです。
間違っていなくて良かったです。
(正確な説明や、理論的・専門的なことを求めている人にとっては しっくりとは こないかもしれませんが)
(訪問者のどんなニーズと この記事がつながるか)
- 消費税の納税と、その仕入控除の意味を知りたい
- 事業の話を聞きたい
- 日記を読みたい
2025年5月11日
プログラミング キャラクタを 3D 化
先月、2025年4月14日の記事で、
>まずは 2D の状態で作って、プログラムを整えてから、3D で作ることを考えています。
と書いていましたが、書いた通り 3D 化を進めています。
2D 版も 3D 版も、HTML/JavaScript によるプログラムです。
ちゃんと 3D で描かれていますね。
◆今回 2D から 3D へ作り直した際の変更点
- 2D だったものは 3D に置き換えられ、
- アニメーションが行われ、
- 照明による陰影も表現されています。
- 顔はテクスチャではなく「線を引く」とかのパス描画で描いています。
ライブラリやフレームワークはいっさい使用せず、自分の計算だけで行っているところがアピールポイントです。
行列計算!!してません! いらないんですよね、本当は。
私も 3DCG のプログラミングはいっぱいやってきたけど、行列計算ってやったことがありません。
使ったことがないので 3DCG 計算において行列を使う理由(メリット)がよくわかりません。
否定しているのではなく、知らないんです。
全然知らないのに、上の動画のような細やかな 3DCG が描けているので、「行列は必要ない」と言うことができます。
行列のメリットを知ればそうは言わなくなるのかもしれませんが…
動画や説明でいろいろ言っても「本当なの?」みたいに疑問は残ると思うので、動画と同じファイルをダウンロードできるようにしておきます。(右下にダウンロードリンク)
ソースコードを見てもらうと行列はいっさい出てこないし、フレームワークへのリンクもありません。
作り途中の物なので、「顔」(面にパス描画)については、試作状態でまとまっていません。
本当はきちんと綺麗にまとめて、入門書のように人々に伝える形を取る予定でしたが、この記事の文脈上の都合で先行公開って感じです。
以下では上記リスト「今回の 2D から 3D へ作り直した際の変更点」の 1 ~ 4 について さわりを説明したいと思います。
(1) 2D → 3D 置き換え
3次元空間の x, y, z 座標を 2 次元座標の h, v に変換するには、
h = x * s / z
v = y * s / z
で計算できます。
(だから行列はいらないのです)
3D を描くために、基本的にはこれだけでいいというのは驚きであり、ありがたいことです。
もちろん、この式以外の「プログラミングのやり方」や「3D 空間の常識」がわりと難しいので、式が簡単だと言っても あなどれません。
詳しくはこのページの上のほうの「Special Documents」のコーナーの「▼3DCG プログラミングの方法」のリンクを見てください。これ
この式での計算は私は数年かけていっぱいやってきたので、今回の 2D → 3D の置換の作業はそんなに大変ではありませんでした。
ある程度プログラミングが出来る人が「3DCG は難しい」と思って取り組まずにいるのはもったいないですね。
(2) アニメーション
3D に限らない話ですが、
「プロパティを現在の値からある値へ変化させる」
という単純な方法で上の動画のように「直立」から「体育座り」へスムーズにアニメーションさせることができます。
たとえばこれ、
この四角形の左上の角の座標 ( x, y ) が 0, 0 で、星の左側のトンガリの座標が 0, 36 だとすると、
x 座標は 0 から 0 へ変化し(同じ)、
y 座標は 0 から 36 へ変化します。
アニメのコマごとに、
x 座標は 0 ずつ変化し(変化しない)、
y 座標はたとえば 2 ずつ変化する。
変化を続けると四角形の左上の座標は最後には星の左側のトンガリ座標と同じになります。
”でも四角形の頂点は4つで、星の頂点の数と違うじゃないか!”
(╬▔皿▔)╯
と思われる方もいると思うので、ダブルクリック(スマホの場合は 2 回タッチ)してください。納得できると思います。
各頂点は変化する先に向かって値を少しずつ変えています。
(3) 照明による陰影
あらわれろ、陰影!
「面が向いている角度によって陰影が異なる」というのは、
「光が当たる方向」と、「面が向いている方向」の「成す角」の大きさを元にすれば表現可能です。
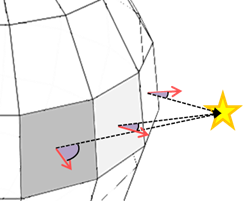
この図で、点線が「光が当たる方向」、赤矢印が「面が向いている方向」です。
光は同じ場所にありますが、面が向いている方向がそれぞれで異なるので、その違いが陰影となってあらわれます。
計算方法
この「成す角」を計算で求めることができれば、面の色をそれに応じて変化させ、陰影を表現することができるようになります。
その計算方法は、、、これを読んでいる人が「分からない」となるのを恐れずに言うと、
a = 面.x * 光.x + 面.y * 光.y + 面.z * 光.z
という、意味は不明かもしれませんが、掛け算と足し算で計算できます。
3次元空間なので、面の中心を 0, 0, 0 の原点として面が向いている方向を x, y, z で(あっちのほうだと)表し、光の方向も同じで x, y, z で表します。
「成す角」が大きければ計算結果の a は小さくなり、「成す角」が小さければ計算結果の a は大きくなります。
「成す角」が小さいということは、光の方向と面が向いている方向がほぼ同じだということでもっとも明るくなります。
▼光の方向と鏡面の方向が一致すると最も明るい(※画像は少し違う例だけど)
全てを理解する必要がない
…とある情報筋によると、この計算は「内積」というのだそうです。
が、私は内積が何なのかは知りません。
知らなくても上の動画のような陰影のプログラミングはできるということです。
(4) 3次元空間内のパス描画
上の動画では、頭の面に顔を描いていて、それはテクスチャではなくパス描画を使っています。
▼パス描画で顔を描いている。 |
▼左:面にテクスチャ貼り、右:面に直接パス描画 (※↑AI画像です) |
普通、3DCG で面に何かを描くと言ったら、それはテクスチャ(画像)の貼り付け(上図の壁に絵を貼るような)で実現するのであり、パス描画を行うというのは私は聞いたことがありません。
しかし、ライブラリやフレームワークを使わない場合、テクスチャを自前で行うのはパソコンの処理速度として限界があるし、テクスチャという技術の具体的な方法も私の勉強不足で分かりません。
パス描画であれば処理速度はあまりかからず、手軽に描画できます。
ここで言うパス描画とは、JavaScript の CANVAS の ~.beginPath()、~.closePath() を使う描画のことです。
JavaScript に限らずとも、どのプログラミング言語でも、ある程度の描画機能はあると思います。
①~③のどの描画も同じパス描画の命令を使っていますが、違うのはそのパス描画命令に渡す座標値が
「2D 平面上の座標」(①)
なのか、それとも
「もとは 3D の座標 x, y, z であり、2D 座標 h, v に変換された座標」(②、③)
なのか、という違いだけです。
パス描画を 3DCG プログラミングで利用すれば、表現力が上がります。
その表現力とは別の話ですが、
▼2D 版の表現力
私はアマチュア(趣味)のプログラマーです。
これは私が作っているプログラムで、アニメで描かれているのは「バク転スワン宙」(地域によってはバク転伸身宙返りなど)と呼ばれる器械体操の技です。
器械体操の経験がある人は、肩で押す、両手で引き上げる、スワンで舞うときは棒のようだ、キマッたら もったいぶって両手を挙げる!というのが分かると思います。
私は中学校の器械体操部のへたくそ部員でしたが、先輩たちの上手なのを間近で見て、顧問の先生(国体選手の方でした)の先輩たちへの指示もいつも聞いていたので、できはしないけど技の細かいところまで知っています。
へたくそなりに、へたくそなバク転を私はやっていました。今思えばよくそんな恐ろしいマネをやってたなと思います。
毎回毎回勇気を出してやっていて、余裕でやってる友達とかとは次元の違う(低レベルで可哀そうな)取り組みだったと思います。
この「バク転スワン宙」のプログラムをここに掲載する理由は、読者の中で「プログラミングを上手になりたい!」と思ってる人がいると思うからです。
プログラミングって難しいですよね。どうやったら学べるのだろうかと。
その解決策の一つがコレなんです。
自分で言うのもなんですが、「目を見張る動き」。
それがこの作品にはあると思います。
もちろん世の中には上には上がいて、私のこのプログラムなんか かすんで見える、もっと優秀な作品がどこかで公開されていると思います。
そういうものへのあこがれが、プログラミングを追いかける原動力になるのではないか、と、そう思うんです。
このプログラムをどう評価するかはこれを読んでいるあなた次第ですが、少しでも感動していただければ幸いです。
(訪問者のどんなニーズと この記事がつながるか)
- プログラミングの話を聞きたい
- 面白いことのあれこれ
- 日記を読みたい
2025年5月16日
生活 最近やっていること(GW)
この前の GW は実家に帰りました。
1/3. 実家のパソコンを整備
父からの頼みで、「会社からもらってきたパソコンを使えるように整備してほしい」ということで、整備しました。
- Windows 10 だったものを 11 にしたり、
- 本体スピーカーなしでしたがモニターのほうにスピーカーが搭載されていたので音声を配線したとか、
- PDF ビューワーを入れたとか、
- メモリ増設は必要なさそう、
- 前パソコンのデータの引っ越し、
…とかそんな感じの整備をしました。
2/3. 房総半島の片倉ダム
片倉ダムというダムを見に行きました。
野生の猿が多めにいて、ダムは放水中でした。
放水の動画、MP4形式/30秒/1080x1920/22.3MB
幾何学的な模様が上から下へ規則正しく流れる様子が面白かったです。
3/3. 茨城県の牛久大仏
全長120メートルの牛久大仏を見てきました。(前にも見ましたが)
大仏の内部に入ることができ、階は 1F~5F まであります。
しかし、わりとどうでもいいような写真がたくさん展示されていたり、今一つの お土産売店があり、大仏の肩のあたりから外を見られる展望台もありましたが、どうも全体的に「チープ感」が漂っており、不満をもらすお客さんがいました。
でもエレベーターのオペレーターをしていた職員のおじさんが、
『大仏の内部は展望台だと勘違いしている人が多いが、実は大仏はひとつの「寺」なのであり、「寺の本堂」が本命です』
と教えてくれて初めて納得できました。
―――それを先に言ってほしい。
1F からエレベーターで一気に 5F まで行き、その後階段降りて 4F。4F からエレベーターに乗り 3F を飛ばして、2F というルートだったかな。3F を飛ばしたときのエレベーターでそのおじさんが話してくれました。
教えてくれた通り、本堂(大仏内部 2F だったかな)は普通の寺らしく、威厳があって良かったと思います。
催し物の主催者は「何が見せ場なのか」を、あらかじめお客さんに正しく知らせる必要があるな、と思いました。
(またはおじさんのように物事の本質を正確にとらえ、そのつもりで催し物全体(大仏内部)をデザインする)
(訪問者のどんなニーズと この記事がつながるか)
- 管理人の見た目の様子
- 最近どうなの
- 日記を読みたい
2025年5月17日
生活 手術予定(そけい部ヘルニア)
今週の木曜日(5/15)、仕事が終わって事業所の門を出たところで、その惨事は起きた!。
股の間に激痛が走り、息が荒くなり動くことができない!
「こっ、これは無理だ」と思って、携帯電話で救急車を呼びました。大変やばかった。
夕方に救急外来で運ばれ、いろいろ診てもらいました。
何が起きたのかというと、ヘルニアですね。
「鼠径部(そけいぶ)ヘルニア」と言って、一般的に「脱腸」と呼ばれるものです。
腸の一部が、「弱くなり穴が開いてしまった筋膜」から脱出して皮膚が腫れる、という病気です。
40歳以上、立ち仕事、過激な運動、肥満という条件を持った男性に多いとか。
(私、今までウエスト76でしたが、(加齢が原因で) 最近は85以上あります)
救急されたその晩は、入院はできないと言われ、帰ることに。
しかし歩くとやばいので、タクシーで帰りました。片道 3,600円。
翌日、同じ病院の消化器科を受診するために家を出ましたが、3分~5分程度歩いただけで激痛の予感がしました。
やっぱり歩けない!
しかたなくまたタクシーを呼び病院へ直行しました。
再度検査して、「手術しかない」という話になり、来週 5/20 に入院?(日帰り手術も可能だそうで入院はしないでしょうね…)
手術後 3 日は仕事は休み、その後は 2 週間経つまでは「座っての仕事」のみ可能。3週間経ったら正常に復帰だそうです。
診察後自宅に帰るときも歩けなかったので、タクシー。往復 8,000 円か。
買い物にも行けないだろうからと途中でスーパーに寄り、タクシーに 10 分待ってもらいつつ買い物。
基本的に私はタクシーの運転手さんとはいつも話をしています。
毎回運転手さんは違いますけど、99%の確率で話をしてますね。
だって何も話さずに沈黙しているなんて気まずいでしょ。
手術でいろいろお金がかかるでしょうけど、保険とか傷病手当でなんとかなるかなと思います。
(訪問者のどんなニーズと この記事がつながるか)
- ハプニングの話
- 最近どうなの
- 日記を読みたい
2025年5月20日
生活 手術日、間違えとった
この前の記事で、今日は手術をすると書いていますが、診察へ出かけたら医師と話が食い違っていて、ただしくは手術日は 6/2(月)でした。
4日間入院しての手術です。
プログラミング キャラクタ 必要な知識体系
またちょっと進みました。
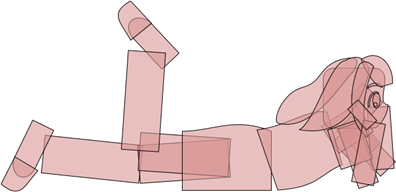
▼前回 |
▼今回 |
前回(左)よりも、今回(右)の方が萌えっとしていて魅力的に見えますね。
◆前回からの変更点
- 前回はカメラの概念が無かったのでズームができなかったが、今回ではカメラの概念を導入したのでズームできるようになった。
- 面に描くパス描画(顔)は moveTo(), lineTo() による直線のみだったが、bezierCurveTo() による曲線も描けるようにした。
- 1つのパーツには1つの 3D モデルしか置けなかったので頭は頭だけだったが、1つのパーツに複数の 3D モデルを置けるようにしたので頭に髪の毛モデルを追加できるようになった。
「前髪を目にかかるくらいに下げたら可愛らしくなった」、というところもあります。
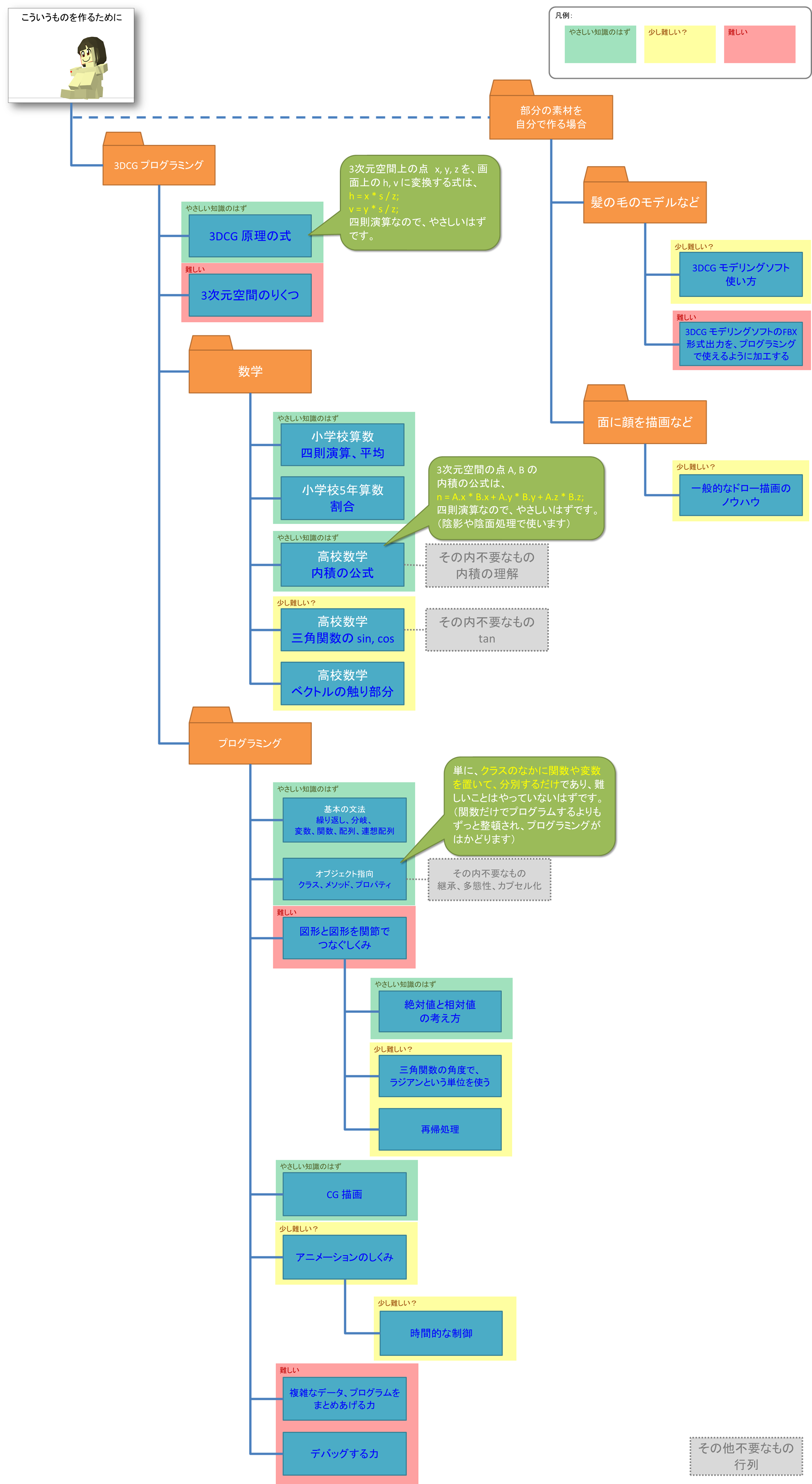
『こういうものを自分も作りたい!』という人のために
こういうものを作るために必要な知識の体系を図にしてみました。(おおざっぱです)
これを見て、だいたいどんな知識を持っていればこういう作品につながるのかを、おおざっぱにでも把握してもらえれば、なんらか道が開けるのではと思います。
(訪問者のどんなニーズと この記事がつながるか)
- 難しいプログラミングの手がかり
- 面白いもの
- 日記を読みたい
2025年5月25日
プログラミング ローカル座標系の不備
今作っているプログラムで以下のような不備が見つかりました。(下図はクリックすると繰り返します)
手を振った後、不備をはっきりと再現するため、腰を反らしています。
その際に両手のひじが伸びますが、伸ばすようにはプログラムしていません。
これが不備です。
(※ときどきポリゴン同士の重なり方がおかしいですが、これは 3DCG 計算の IC (CPU 内の専用ルーチン) を使わないで 3DCG を手計算でプログラミングする際の限界です)
「上腕」パーツ(ひじから上)と「前腕」パーツ(ひじから下)は「ひじ」コネクタでつながっています。
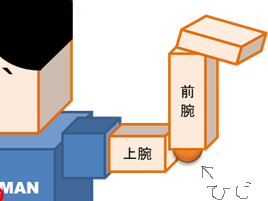
原因は、「子パーツ(前腕)の角度が親パーツ(上腕)の角度(上腕のワールド座標の角度)から影響を受けてしまっている」ということで、正確に言うと「ローカル座標の考え方がうまくいっていない」ということです。
ローカル座標とは、
『肩やその他 身体の各部位の角度がどうあろうと、ひじが90度の角度を持っているなら、ひじという場所においては局所的に90度として見る』
というもので、それに対してワールド座標(絶対的に見た角度)とは
『肩が90度の角度を持っていて、ひじが90度の角度を持っているなら、ワールド座標におけるひじの角度はこの2つを足して180度だ』
というものです。
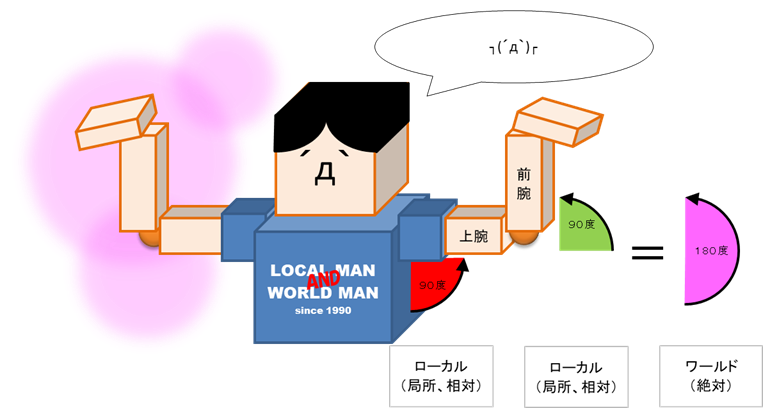
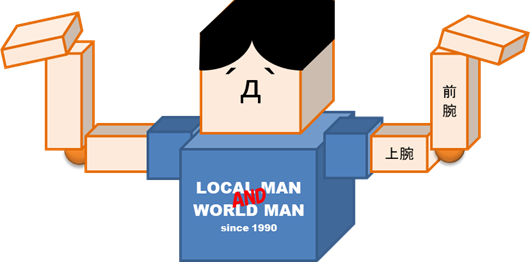
体育座りしている状態で、両ひじはローカル座標として局所的に90度の角度を持っています。
ところが腰をそらしたというだけで、この局所性(ローカル座標)が壊れて、0度へ動いてしまっています。
私の計算が普通に間違っているんですね。
前の記事の「知識の体系」の やさしい知識のはず 絶対値と相対値の考え方 とした知識がこれです。
絶対値=ワールド座標で、相対値=ローカル座標です。
やさしいはずですが、知識の体系の1つ上の段階では 難しい 図形と図形を関節でつなぐしくみ と書いています。
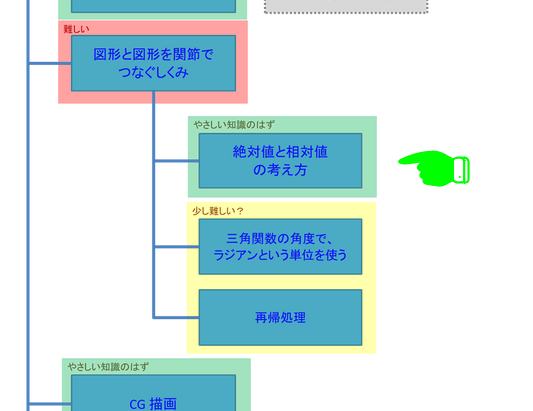
絶対値と相対値
絶対値(=ワールド座標)とは下表のように、1~10まで普通に数えることを言います。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
相対値(=ローカル座標)とは、この↑黄色の部分について、あらためて、
| 1 | 2 | 1 | 2 | 3 | 4 | 7 | 8 | 9 | 10 |
局所的に1~4まで数えることを言います。
局所的には1番でも、全体的には3番ですよ、と言えます。
たとえば、ひじを局所的に90度曲げたということは、絶対的には(肩の曲がり90度のことも考えて)180度になるということに相当します。
ひじだけを見て「90度曲げる」と言うことができれば、人間の感覚的に操作が便利なんです。
そのための絶対値、相対値です。
絶対値、相対値、自体はそんなに難しくない考え方ですが、3DCG であり、親子関係が複雑だと落ち着いて整理して考えるのがとても難しいんです。
で、このローカル座標の計算のしかた(私の認識)が間違っていたということで、
ローカル座標についての考え方を別途、試作することにしました。
メインのプログラムの問題について、別途新しいプログラムで試作を作ることは有効なんです。
余計なことを考えないで、問題に集中できるからです。
それでも結構大変だったんですが、下図のように試作ができました。
赤が親で緑が子。そしてまた緑が親となり、その子として青があります。
赤は角度(水平方向の角度、向かって左右の傾き)を持っていないので0度です。
緑は赤に対してローカル座標として15度の角度を持っています。赤が0度なので、0度+15度でワールド座標としても15度です。
青は緑に対してローカル座標として問題なく回転しています。
青の回転は、緑が回転しても、赤が回転しても、乱れることはありません。
(↑このリンクは繰り返しクリックできます。遠近を濃淡で表現していないので目が混乱すると思いますが)
ちゃんとローカル座標が実現されています。
どう解決したのかというと、

考えるしかないんですが、寝ても覚めても2つの直方体の角度や回転などの位置関係、計算手順を考えるんです。
その仕事に従事している人は、誰よりもその仕事について深く考えることができるはずです。
その仕事に従事していない人は、その仕事について考えることはできません。
趣味も仕事も最初は簡単なところから始めて、進んでいきます。
その先にあるのが難しい考え事です。
「経験しなさい」というのはよく言われることですが、どこか教育じゃない(何も教えていない)気がするので、
を参照できるようにしておきます。
ある程度まとめはしたけど、あくまでも自分用(私用)なので、一部分かりづらい表現もあるかもしれません。
この試作を元の人間のプログラムに当てはめたいんですが、人間のプログラムは複雑で当てはめるのは難しいので、人間のプログラムをまた1から作り直すことにしています。
設計の甘さがプログラム全体をダメにする良い例ですが、個人の趣味なのでそれでいいんです。
仕事でそれをやるとやばそうだけど。
(訪問者のどんなニーズと この記事がつながるか)
- バグとその原因、解決の話
- 面白いものを見たい
- 日記を読みたい
2025年5月29日
AI みんなが同じ知識量に。
そう思ってこんな図を作ってみました。
この図では「AI によりみんなが同じ知識量になっている」ことを示しています。
ちょっと独りよがりかもしれませんが、本質的なところは突いているんじゃないかなぁ…と思います。
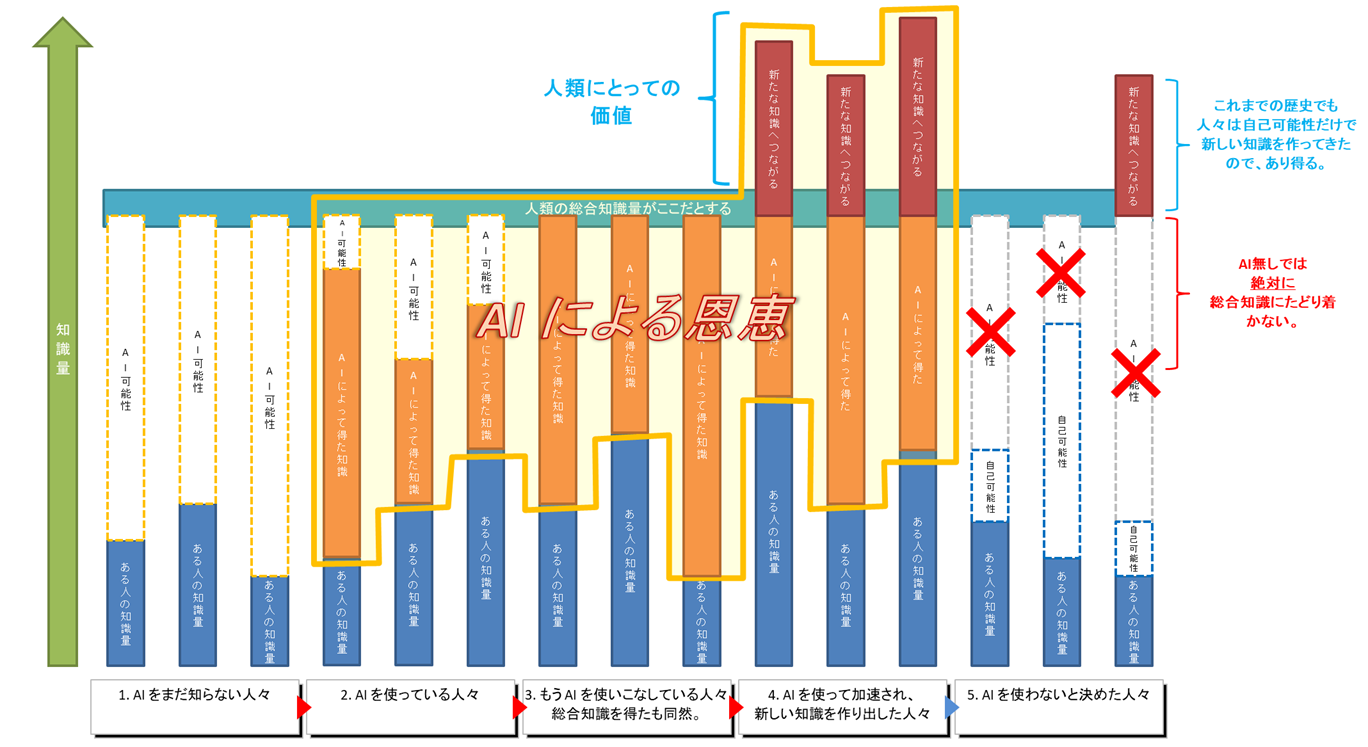
以下は図(グラフ)の説明です。
このグラフは、個人個人が持っている知識量(下部にそれぞれ並んだ青い部分「ある人の知識量」が、AI により補強される様子)を示したものです。
AI の登場により、人類が持っている知識のすべて(グラフ上部の水色の総合知識量のバー)に、アクセスできるようになりました。
そして、AI を使うことにより、基礎的で広範な知識を得ることができ、それによって新しい知識へとつながり得ます。(総合知識量のバーを越えた赤い部分「新たな知識へつながる」)これは公的に技術者たちが期待している部分だと思います。
人々は、グラフの左側から右側へ遷移します。(人によっては最終的に AI を使わないと言い始める人もいるかも)
- 「AI をまだ知らない人々」は、AI をこれから使って質問さえすれば、オレンジ点線の「AI可能性」で示される通り、人類の総合知識をその場で得ることができます。
- 「AI を使っている人々」は、すでに多くの知識をその場で得ており、もっと上手に使いこなせば、人類の総合知識にアクセス可能です。
- 「もう AI を使いこなしている人々」は、総合知識を得たも同然で、「なんでもできる」と言えます。
絵とか、運動とか、プログラミングとか、上手に質問して、コツを得て、体得・習得ができるはずです。 - 「AI を使って加速され、新しい知識を作り出した人々」は、AI が無ければ知識量は一定でとどまっていたはずですが、AI によって知識が補強され、新しい知識(グラフの上部の赤い部分)を見つけるに至った人々です。
- 「AI を使わないと決めた人々」は、AI による恩恵「AI 可能性」を「いらんです」と受け取らない人々です。
そういう人たちはこれまで通りの自分の力「自己可能性」(青い点線部分)で前に進み、「私一人の力はこれだけある」と喜ぶ人々です。
しかし AI 無くしては、「81億人、数千年の歴史」である「人類の総合知識」に至ることは絶対にないのは誰でも分かります。AI 無しでどうやってすべての知識にアクセスするんでしょうか。
その知識を「いらない」ということの意味は深くて難しいところだと思います。
AI が持っている知識はデータベースの中にある量を超えることは無く一定であり、人間は質問さえすれば、自由にその知識にアクセスできます。…というようなことを図で表したつもりなんですけど、、
AI がデータベースの中に持っている言葉が仮に 100 個あるとして、その1つ1つについて他の 100 個の言葉への確率が付与されている(AI 技術のもと)。100 個に対する 100 個の組み合わせは、100 x 100 で 10,000 通り、で良いんでしたっけ。(数学の「組み合わせ」は苦手で…)
とにかく組み合わせは上限があり、知識量は一定だということです。説得力がないですねえ…
ところで私はグラフの 5 番の人(AI を使わないと決めた人々)ですが、
AI の問題点:
- 自分で考えずに AI を利用することで、考える力が減退する。
- 人と人との交流(教わる)が減る。
- 創作物のオリジナリティが無くなる。(自分の力で作ることの喜びが減る)
- 犯罪に使われている。
「向こう10年これらは解決されないだろう」という私自身の予想を信じて、多大な魅力の知識に触らずに、「やってみるか、、」と独り進むことにしています。
損するかもしれないけど、得もあると思うんだ。
(パワー満点の焼肉弁当を取らずに、地味で落胆しそう・でも滋養味豊かな幕の内弁当を取る。この話はイケイケの若い人たちは聞くことができないだろうな。そんなにいっぱいの具 (幕の内弁当は具だくさん) は必要ないとか言って)
まぁ、みなさんにとっては、全否定してもしょうがないのでほどほどに使うのがベストかな。
(訪問者のどんなニーズと この記事がつながるか)
- AI 利用の倫理
- AI の話
- 日記を読みたい
パソコン Firefox の新規タブの壁紙
窓の杜でこのようなニュースがありました。
新規タブに壁紙を設定できる「Firefox 139」が正式リリース
インターネットブラウザのひとつ「Firefox」の新規タブに壁紙が設定できるそうです。
▼Firefox の新規タブ(旧) |
▼Firefox の新規タブ(新) |
これはバージョン 139 で試験的に搭載された機能で、設定のページの「Labs」で設定できるということです。
しかし、私が使っている Firefox にはその Labs が見当たりませんでした。
(※ スクリーンショットの右下に見える小さなタブはセキュリティソフトの機能です)
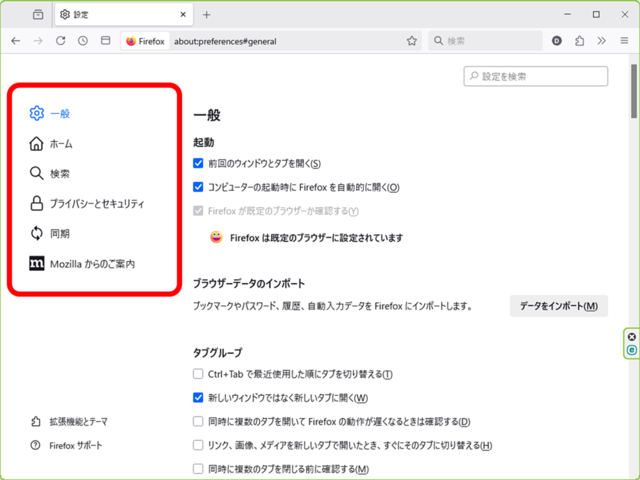
左上図のこの欄に「Labs」があるはずですがありません。
どういうことなのでしょうか??
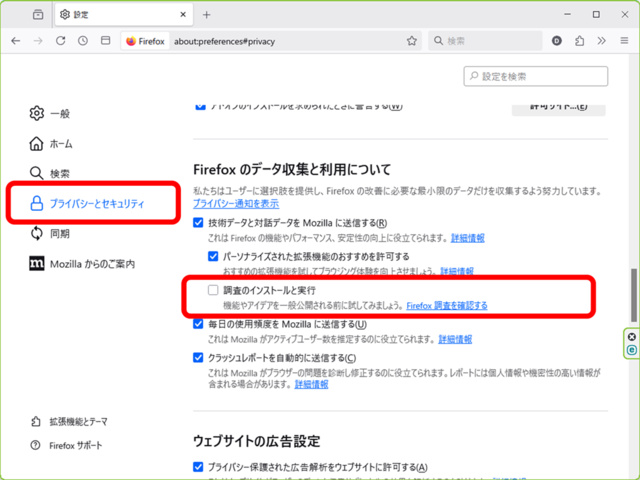
「プライバシーとセキュリティ」をクリックし、
この「調査のインストールと実行」のチェックが外れていることが原因でした。
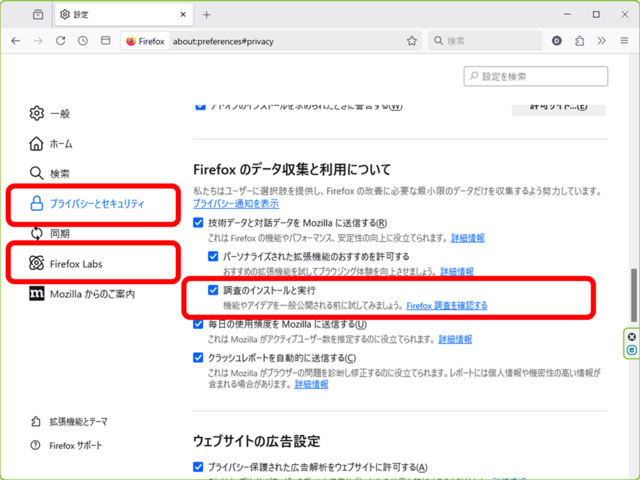
チェックを入れると、Labs が現れます。
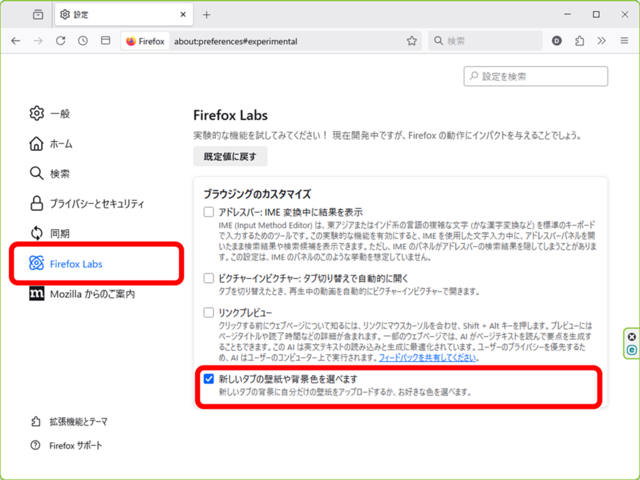
「Firefox Labs」をクリックし、
「新しいタブの壁紙や背景色を選べます」にチェックを入れます。

そして、新しいタブを開いて、右下の歯車アイコンをクリックします。
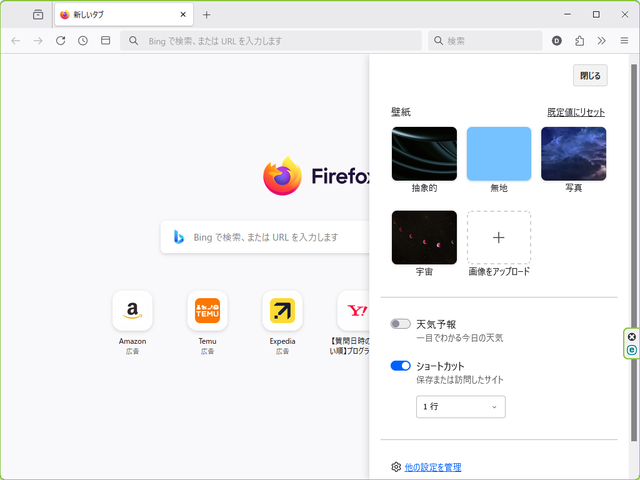
すると壁紙の設定画面が現れます。
ここで壁紙を選ぶと…

新しいタブの壁紙が設定されます。
壁紙があるほうがずっと良いですね。
…自分の画像ファイルを壁紙にできるといいなと思ったんですが、それはできませんでした。
(訪問者のどんなニーズと この記事がつながるか)
- 試験機能を設定する Labs がない、どうすればいいのか
- Firefox の新規タブに壁紙を設定したい(試験機能)
- 日記を読みたい
2025年5月31日
知恵袋 最近の私の回答
Yahoo!知恵袋では、「ある人」を指定してその投稿内容を探し出すことができません。
私がどんな回答をしているのか、リストアップして見ることはできないんですね。
なので、自分のホームページでリストを示すことになります。
私の知恵袋でのアカウント名は「平行四辺形」です。
私の本名のイニシャルが D.K なので、最初は「台形」という名前にしていました。
理由あって、台形を自分でアカウント削除(そのときカテゴリマスターの称号がありましたが、あまり興味ないので構わず削除)し、図形つながりで「三角形」とするがそれも削除、その後、やはり図形つながりで「平行四辺形」としたわけです。
誰かが名前として使い始めると、たかが算数・数学の「平行四辺形」もどこかキャラっぽく見えてしまうもんですね。
▼平行四辺形アカウントのアイコン

新しい順にベストアンサーを3つほど。
- C言語関連
オブジェクトという言葉は英単語として訳すと、 >(知覚できる)物、物体、対象、目的、目標、おかしなもの、目的語、客観、客体 (Weblio 辞書)…
回答数9 5/24 23:20 - プログラミング
暗号化することをエンコーディングと言います。 特にデジタルデータでは「何か目的があって」データを変換することを言います。 たとえば、『データ量を減らした…
回答数7 5/23 1:40 - プログラミング
少し長くなりました。スミマセン。 まじめな人の投稿ですが気楽に読んでください。 ・行った方がいい、役に立つ高校、大学(全日制、通信制etc…) 工…
回答数5 5/19 19:24
まだ「回答受付中」のものを新しい順に3つほど。
- C言語関連
10 行目の何もないところに、 #define n 100 と書いて、 12行目の int n; と 15 行目の scanf_s の…
回答数6 5/31 12:25 - JavaScript
こんな感じになります。 <!DOCTYPE html> <html> <head> <title>&…
回答数2 5/31 9:22 - 祭り、花火大会
リッツパーティーと、室町幕府の誕生日にケーキを買って個人的に楽しむ祭。 今日は何年目のWindows95の発売日だからお祝いしようってよくやるでしょ。…
回答数3 5/31 8:08
がんばって回答したけど…というものをピックアップ
- C言語関連
アスキーアートみたいなので良ければ、こんな感じ? #include <iostream> #include <cmath>…
回答数4 5/27 9:52 - C言語関連
C言語や C++ に特有の「ポインタ」については大丈夫ですか? 「ポインタ」を克服すると上達につながります。 案ずるよりも生むがやすしです☆彡 (でも難し…
回答数5 5/27 12:16 - YouTube
板状の直方体に三角すいが突き刺さったとき、三角すいの先端が直方体の向こう側へ突き抜けるけど、その先端を表示しないほうが自然だ、それは難しいのか?という話ですよね…
回答数6 5/28 12:21
で、盛況なのかなと思われるかもしれませんが、あんまり盛況じゃないです。
(※ BA = ベストアンサー)
▼次のグレードまで 254 BA…道は長い。 |
▼BA 率は 65% 前後ですが… |
▼私が欲しいのは BA じゃなくてコレです。 |
リアクションの
「そうだね。君の言っていることは確かにそうだよ。」
というのがすくねえっす。いやいや、
「なるほど、そうなんだね、知らなかったよ。」
と言われてる件数が、回答総数 723 件中、600 件(1 回答あたり複数のなるほどもありうる)あるので、なるほどザワールド君ってかんじ。
このホームページの内容もなるほどザワールドと言われかねない。
で、何が不盛況なのかというと、返事が無いんですよね。
BA はあっても無言の BA。
普通は、「ありがとうございます!めっちゃわかりやすかったです!嬉しいです!解決しましたアメアラレ!」となって良いと思うんですけど、無言無言のゴンゴンゴン。
私の回答って、なんなんだろうな…。
いろいろ調べ上げて、確かなところを厳選して、確かに役に立つようにと、回答しています。
それでも質問者さんから見れば、的を外していて、でも頑張って書いているようで、間違ってもいないようだから BA、って感じなのかな。それとも、ゆき届きすぎて引いてるのかな。そこまでやらなくてもと。
あと日本語はあまり得意ではないので、ちょっとでも意味が不明になるとダメなのかもしれません。
でも、私が質問者だったら、回答者全員に対して、しっかりと返信を行い、ち密に審査して BA を厳選し、BA お祝いメッセージ欄では「どこがどう役に立ったのか」を書くし、おしくも BA にならなかった人にも感謝の意を述べます。
私の質問を新しい順に3件ほど。
- 将来の夢
生成AIについて質問です。 生成AIは人々の創作の夢を奪うと思うのですが、どう思いますか? 創作の夢とは、 ・誰かの絵に憧れて私も描きたいと心から願う、 ・自…
回答数8 3/31 6:28 - シニアライフ、シルバーライフ
年配の方にお聞きします。 最近の若者について、好きなところを教えてください。 (私は50歳です) 若者の人も「答えたいんだぜ?」みたいな人がいたら可です。...
回答数1 2024/12/27 12:32 - 料理、食材
汁ものを器にいれてラップをして電子レンジに入れて温める時の、ラップをかける意味(科学的根拠)を教えてください。 蒸気が庫内に充満してしまうのを防ぐため、蒸...
回答数4 2024/10/20 9:30
それはやりすぎではなく、普通だと思います。
返信なしだなんてありえなくて、特に数人が回答している中、一人だけ返信しないと言うのも可哀そうすぎて絶対にできません。
…でも、質問すると分かりますが、回答者一人一人のそれぞれで言葉に偏りのある話(ぶっちゃけて言うと、説明文の意味が全然分からないことがある)をよく読んで意味をしっかり理解して、意味のある返信を書くというのは簡単ではありません。
なので私の長文に対して返信が無いとか、BA が無言だとか、私自身である程度は理解できていると思います。
「無言の BA」。ポップスの曲名かい。
♪~ランランララ、
無言の無言で無言よほーいほい
書きます書きますどこまでも
バババと行こうぜBA、BABABA!
~ルー、ランララ
無言でラララ。
…最後の1行がさびしい~
歌に歌うほど理解があるってことです。
この歌の出典(まねのもと)が一応ありますね。

故 J.H.ブレナン グレイルクエスト/ドラゴンファンタジーシリーズ、
①「暗黒城の魔術師」(CASTLE OF DARKNESS)
④「七つの奇怪群島」(VOYAGE OF TERROR)
⑤「魔獣王国の秘剣」(KINGDOM OF HORROR)
⑦「幻し城の怪迷路」(TOMB OF NIGHTMARES)
などなど。
読む人を選ぶところがあるかもしれないけど、タイトルがカッコよく、表紙のイラストも質が高い。本文の挿絵は表紙と違いクロッキー風でホラー感が強い。本文の指示に従って読者の意思で物語の道筋を選ぶことができるゲームブックです。
これらのシリーズすべてに登場する「魔人」というキャラが、この手の詩(歌)を歌うんですね。
さらにこの手の歌がどこから来たのかというと、どうも J.R.R トールキンの「指輪物語」っぽいんですよね。「指輪物語」では似たような調子で詩が歌われます。
この二人の著者はどちらも児童向けに物語を作っていたので、詩の内容も大人向けではないんです。
J.H.ブレナン 氏はイギリスの人で、日本の読者限定でメッセージを送ってくれています。(左上図、1985年)
まぁ、それはともかく、
私の回答の目的は人助けです。
たとえば、IT 関係で力ない質問者を笑う回答者がいたりして、そういうのを見ると特に助けたくなります。
誰であろうとやさしく丁寧に教えれば、どこまでも育つと信じている、、ではなく、それは私の中で真実となっているんです。
猫の話ですけど、一度も怒らずに育てたら、そのにゃんこは私とのあいだに人間と同等のコミュニケーションを獲得しました。
- 抱っこしてたところ、腕に軽くかみついた。「おろしてくれ」というメッセージであり、これまで一度も(1年半くらい)かみついたことは無かったのでそれは間違いない。
- 近所のボス猫に追いかけられていたところ(私ではなく猫が。です)、私のそばを通り過ぎるとき「ニャ」と小さく合図を送ってきた。私は後を追いかけて行った。
- 私が寝床で寝ていたら近くまで来てニャーンと鳴いた。私は「分かったよ」と言って窓を開けた。鳴いたときの顔が人間の子供が親にお願い事をするときの顔とまったく同じだったので、私はショックを受けてしばらく寝床でぼうぜんとしてしまった。
聞いた人は私から何度も聞いた話だと思いますが、優しいことにより、人間と同等の成長が動物にさえあるんです。
仕事とかでみなさんも経験はあると思いますが、優しくない人から教わることはほんのちょっとでしかないです。優しければもっと教えてと頼めるし、怒らないから同じことでも何度も何度も聞き返すことができます。
繰り返し繰り返し教えることで身に付くんです。

(訪問者のどんなニーズと この記事がつながるか)
- 回答の目的は
- 日ごろどんな知恵袋回答しているの
- 日記を読みたい